Coordinates Of A Unit Circle

Unit of measurement Circle Computer

Created by Hanna Pamuła , PhD candidate

Reviewed by

Dominik Czernia , PhD and Jack Bowater

Last updated:

Oct 14, 2022

Table of contents:

What is a unit circle?
Unit circle: sine and cosine
Unit circle tangent & other trig functions
Unit circle nautical chart - unit circle in radians and degrees
How to memorize unit of measurement circle?

Welcome to the unit circumvolve calculator ⭕. Our tool will assistance you make up one's mind the coordinates of any point on the unit circle. Just enter the angle ∡, and we'll prove you lot sine and cosine of your angle.

If you're not sure what a unit circle is, scroll down and you lot'll notice the respond. The unit circle chart and an explanation on how to find unit circle tangent, sine, and cosine are also hither, so don't wait whatsoever longer - read on in this cardinal trigonometry estimator!

What is a unit circle?

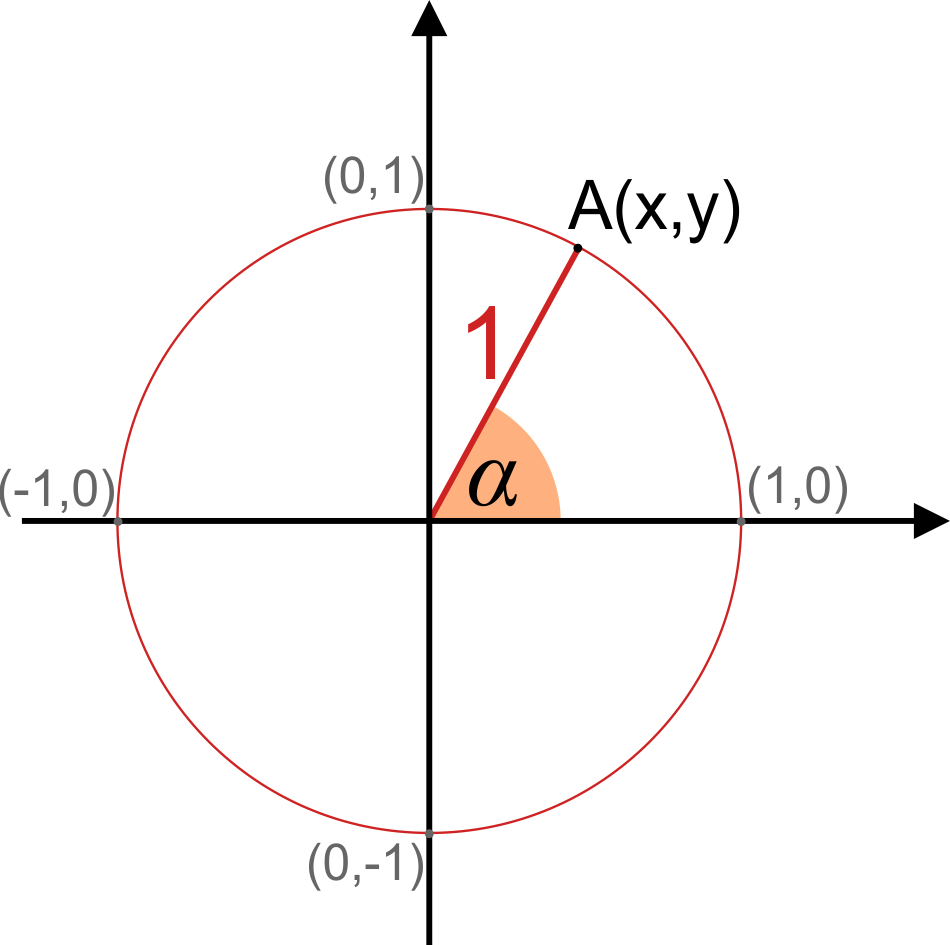
A unit circle is a circle with a radius of 1 (unit radius). In nigh cases, it is centered at the point $(0,0)$ , the origin of the coordinate system.

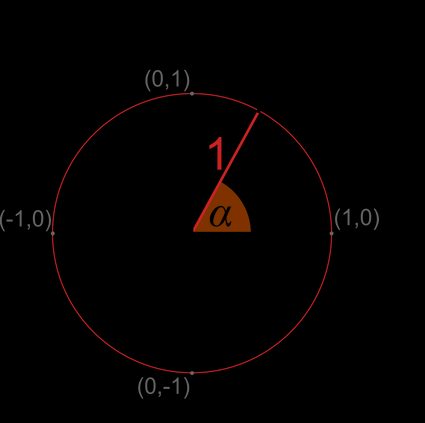
Unit circle is a actually helpful concept when learning almost trigonometry and angle conversion.

At present that you know what a unit circle is, let'due south proceed to the relations in the unit circle.

Unit circle: sine and cosine

OK, so why is the unit of measurement circle so useful in trigonometry?

TL;DR
Unit circle relations for sine and cosine:

Sine is the y-coordinate; and
Cosine is the x-coordinate

🙋 Do you need an introduction to sine and cosine? Visit our sine calculator and cosine calculator!

Standard caption:

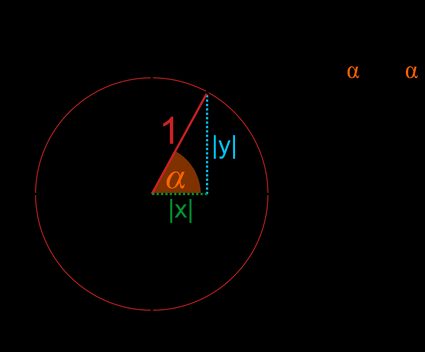
Let's have any indicate A on the unit circumvolve's circumference.

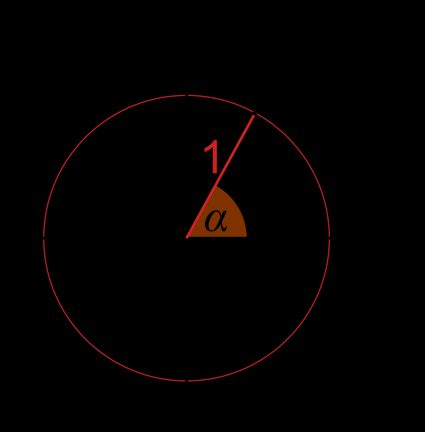
Unit circle in a coordinate system, with point A(x,y)

The coordinates of this signal are $x$ and $y$ . As it's a unit circle, the radius r is equal to $1$ (a altitude betwixt point $P$ and center of the circle).

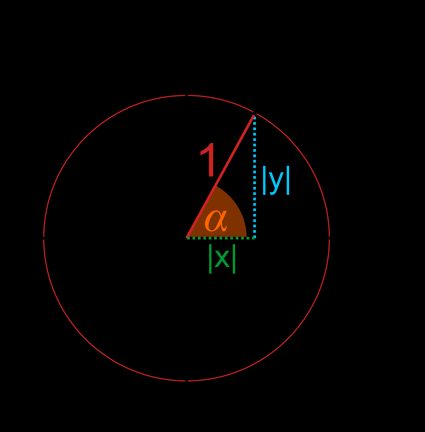
Unit circle in a coordinate system with point A(x,y) and legs |x| and |y|

By projecting the radius onto the x and y axes, we'll get a right triangle, where $|ten|$ and $|y|$ are the lengths of the legs, and the hypotenuse is equal to $i$ .

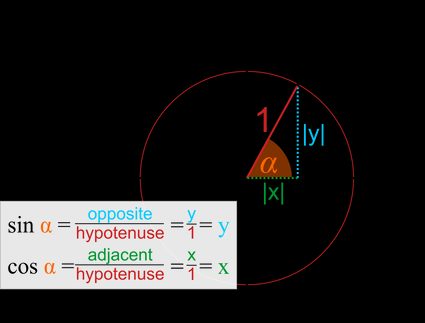
Unit circle in a coordinate system with sine and cosine formulas.

As in every correct triangle, y'all can determine the values of the trigonometric functions by finding the side ratios:

$\sin(\alpha)=\frac{\mathrm{oppostie}}{\mathrm{hypotenuse}} = \frac{y}{1} = y$

And so, in other words, sine is the y-coordinate:

$\cos(\blastoff) = \frac{\mathrm{adjacent}}{\mathrm{hypotenuse}} = \frac{x}{1} = x$

And cosine is the x-coordinate.

Unit circle in a coordinate system with point A(x,y) = (cos a, sin a)

The equation of the unit circle, coming directly from the Pythagorean theorem, looks as follows:

$x^two+y^2=1$

Or, analogically:

$\sin^2(\alpha) + \cos^2(\alpha) = ane$

🙋 For an in-depth analysis we created the tangent calculator!

This intimate connection between trigonometry and triangles can't be more surprising! Find more nigh those important concepts at Omni's correct triangle figurer and Pythagorean theorem calculator

Unit of measurement circle tangent & other trig functions

You can find the unit circle tangent value straight if you call back the tangent definition:

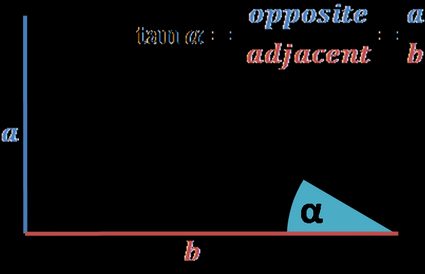
Right triangle: illustration of the tangent definition. Opposite side over an adjacent.

The ratio of the reverse and adjacent sides to an angle in a right-angled triangle.

$\tan{\alpha} = \frac{\mathrm{opposite}}{\mathrm{adjacetn}}$

As we learned from the previous paragraph, $\sin(\alpha) = y$ and $\cos(\alpha) = x$ , so:

$\tan(\alpha) = \frac{y}{x}$

Nosotros can also ascertain the tangent of the angle as its sine divided by its cosine:

$\tan(\alpha) = \frac{\sin(\alpha)}{\cos(\blastoff)} = \frac{y}{x}$

Which of grade will give us the same effect.

Another method is using our unit circle estimator, of grade. 😁

Merely what if you lot're not satisfied with but this value, and you'd similar to really to see that tangent value on your unit circle?

It is a bit more tricky than determining sine and cosine - which are merely the coordinates. There are two ways to show unit circle tangent:

Method 1:

Create a tangent line at point $A$ .
It will intersect the x-centrality in point $B$ .
The length of the $\bar{AB}$ segment is the tangent value

Method 2:

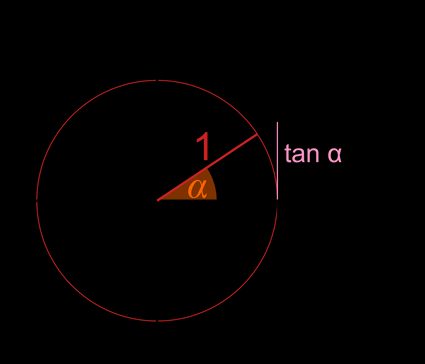
Draw a line $x = 1$ .
Extend the line containing the radius.
Proper name the intersection of these two lines as point $C$ .
The tangent, $\tan(\alpha)$ , is the y-coordinate of the point $C$ .

In both methods nosotros've created right triangles with their side by side side equal to one 😎

Sine, cosine and tangent are not the only functions you tin construct on the unit of measurement circle. Apart from the tangent cofunction - cotangent - you lot tin also present other less known functions, east.yard., secant, cosecant, and archaic versine:

Circle-trig6 — Graphic by Steven Chiliad. Johnson at English Wikipedia, CC BY-SA.

Unit circle chart - unit circle in radians and degrees

The unit circumvolve concept is very of import because you can use it to the observe sine and cosine of any angle. We present some normally encountered angles in the unit of measurement circle chart below:

As an example - how to determine $\sin(150\degree)$ ?

Search for the bending $150\degree$ .
As nosotros learned before - sine is a y-coordinate, and then we take the 2nd coordinate from the corresponding signal on the unit circle:

$\sin(150\degree) = \frac{one}{2}$

Alternatively, enter the angle 150° to our unit circumvolve calculator. We'll evidence you the $\sin(150\degree)$ value your y-coordinate, too every bit the cosine, tangent, and unit circle chart.

How to memorize unit circle?

Well, it depends what you lot desire to memorize 🙃 In that location are two things to remember when it comes to the unit of measurement circle:

Angle conversion, so how to change between an bending in degrees and ane in terms of $\pi$ (unit circumvolve radians); and
The trigonometric functions of the popular angles.

Allow's commencement with the easier first role. The almost important angles are those that you'll use all the time:

$30\degree = \pi/6$ ;
$45\degree = \pi/4$ ;
$sixty\degree = \pi/3$ ;
$xc\degree = \pi/2$ ;
And total bending, $360\degree = 2\pi$ .

As these angles are very common, endeavor to learn them past heart ❤️. For whatsoever other angle, y'all can employ the formula for angle conversion:

$\alpha\ [\mathrm{rad}] = \frac{\pi}{180\degree}\times \alpha\ [\mathrm{deg}]$

Conversion of the unit circle's radians to degrees shouldn't exist a problem anymore! 💪

The other role - remembering the whole unit of measurement circle nautical chart, with sine and cosine values - is a slightly longer process. Nosotros won't depict information technology here, simply experience costless to bank check out 3 essential tips on how to call up the unit circle or this WikiHow page. If you prefer watching videos 🖥️ to reading 📘, watch 1 of these two videos explaining how to memorize the unit of measurement circle:

A Fob to Call up Values on The Unit Circumvolve; and
How to memorize unit circumvolve in minutes!!.

Also, this tabular array with unremarkably used angles might come in handy:

$\mathrm{\boldsymbol{\alpha}}$ (bending)		Trigonometric functions
$\mathrm{deg}$	$\mathrm{rad}$	$\sin(\alpha)$	$\cos(\alpha)$	$\tan(\alpha)$
$xxx\degree$	$\pi/six$	$1/2$	$\sqrt{three}/2$	$\sqrt{3}/3$
$45\degree$	$\pi/4$	$\sqrt{2}/2$	$\sqrt{2}/2$	$1$
$60\degree$	$\pi/iii$	$\sqrt{three}/2$	$1/2$	$\sqrt{three}$

And if whatever methods neglect, feel free to utilise our unit of measurement circle estimator - it's hither for yous, forever ❤️ Hopefully, playing with the tool volition help yous understand and memorize the unit circumvolve values!

Hanna Pamuła , PhD candidate

Unit circle in a coordinate system with Pythagorean trig identity formula.

Arccos Arcsin Arctan … xvi more